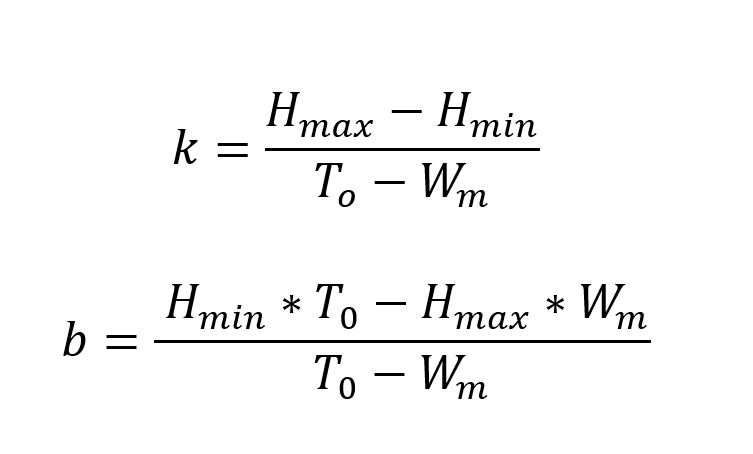The proximate mechanisms behind fear: an IBM approach to understanding behavioral changes in songbirds and the subsequent evolutionary trajectory
Published · Updated

A report written by Hanif Kawousi, Sergey Budaev and Jarl Giske
Abstract
In this article, we present an individual-based model (IBM) investigating the proximate mechanisms behind phenotypes “boldness” and “fearfulness” in songbirds. Two selection pressures, “hunger” and “predator-induced risk”, are reflected in the genotype of the model’s digital songbirds. In our model, these two emotions work as opposites: when the songbirds are hungry passed a certain point, they are not afraid of predation and vice versa. Ergo, the genes dictate the hard limits for the phenotypic variations possible. Other limitations, such as bird mass and environmental factors, affect them as well. By running the model code through many generations of a population of songbirds, we investigated how these phenotypes evolved despite limitations, and which one(s) would become predominant in our population. Our results show rapid evolution, despite the limitations of bird mass set by the algorithm. The phenotype expressed as “moderate amount of fear” became predominant before ten generations had passed. For the future, we propose further development of the model, as it is quite simplistic. Still, we believe this can add to the explanation of proximate mechanisms behind phenotypes, as well as satisfy the demands of ethical practice regarding animal welfare in science.
Introduction
Since the publication of The Origin of Species (Darwin, 1859), the study of animal behavior has revolved around the idea that behavior has evolved through adaptation. For nearly a century, quantitative evolutionary ecologists have simplified the inquiry into adaptive behavior by focusing on the concept of optimal behavior (Fawcett et al., 2013; Lotka, 1925). Darwin’s theories were presented in the form of the English language and not numerically through mathematics. Therefore, in the past century, mathematical models have been developed in an effort to describe these theories. In the pursuit of modeling behavioral ecology, inspiration was drawn from other disciplines such as physics, and its presumed simplifications of natural phenomena, and economics, with its concepts of costs and benefits. Both, as described below, valuable concepts regarding optimization methods in behavioral ecology.
The primary issue with a mathematical approach was the simplification needed to explain evolution. This need for simplification was addressed by Alfred Lotka in 1925. Lotka was the first to model evolutionary adaptation and behavior, by turning Euler’s population growth equation (1767) into an equation for fitness, now known as the Euler-Lotka equation (Lotka, 1925). Here, Lotka willingly simplified nature by combining the anatomy, behavior, and life history of an organism into a common currency, describing all that either adds to or diminishes an individual’s reproductive rate (r) during a lifetime. Due to the lack of computational technology at the time, these calculations were intentionally made to reach a point of optimal behavior in animals, stripped of realities’ imperfect nature and complexity. In this way, numbers could be easily produced and used in the early models.
The implementation of optimization methods, to forecast how organisms would optimally respond to environmental factors (Fisher, 1930; Lotka, 1925), was therefore both willingly and knowingly done without accounting for the constraints usually present in nature. Still, as those who model nature must keep in mind, these constraints are highly present in the lives of real-life organisms: Imperfect information, lack of analytical skills, limited foresight, physiological and cognitive limitations, etc. Consequently, while modeled organisms may use all relevant environmental and physiological information to assess and determine the behavior that would contribute the most to fitness, real organisms must contend with many inherent limitations, the above-mentioned included.
More than half a decade later, Allen Grafen built upon William D. Hamilton's influential work (Hamilton, 1964a, 1964b, 1970) and proposed the concept of the "phenotypic gambit" (Grafen, 1984). A “Gambit” is a term originating from the game of chess, representing the sacrifice of a smaller component for an advantageous, larger gain. The phenotypic gambit is in this way designed to "sacrifice" the proximate mechanisms (i.e., genes) for the advantage of not having to do genetics when exploring phenotypes. Despite the continuing increase in computational power available to behavioral ecologists, the simplification does little, if anything, to reveal the mechanisms behind the phenotypes examined.
This presents us with a paradox within evolutionary ecology. Behavioral ecologists have dedicated substantial efforts to devising complex theories and models that identify the behavioral strategies anticipated to optimize lifetime fitness under certain constraints. Contrary, the field of evolutionary ecology remains largely unexplored in terms of shedding light on the proximate mechanisms behind decision-making processes or the specific implementation of fitness maximization within the nervous system (Budaev et al., 2019; Fawcett et al., 2013). The paradox is enforced by the fact that, unlike the assumptions of early models of animal behavior, all nature’s solutions have been restricted by proximate mechanisms, i.e., genetic limitations to phenotypic expressions (Andersen, 2014).
The model presented in this article also provides additional push-back against the phenotypic gambit by showing that a single gene can be expressed through a range of phenotypic expressions, meaning plasticity. Phenotypic plasticity is how a gene “comes to show”: a manifestation formed not only by its genetic architecture but also by the environment surrounding it (Scheiner, 1993; Via & Lande, 1985). In our model, the songbird is given a single gene. However as shown in the Results section, this single gene can provide a range of phenotypes. Even if they are genetically limited, these results help to solve the above-mentioned paradox. Where the phenotypic gambit intends for the proximate mechanisms to be sacrificed in pursuit of showing fitness by phenotypes, we provide results indicating otherwise.
Modeling Songbirds
In nature, it is shown that the sound of predators alone is sufficient to make songbirds produce fewer offspring (Allen et al., 2022). In their paper, Allen and co-authors showed that through intermittent broadcasting of predator sounds, the fear produced in songbirds were sufficient to cut the population in half after five generations. While the ultimate explanation based on phenotype in their paper is clear, it is not clear how the genetic constraints nor the phenotypic plasticity affected survival. Why did some songbirds make better choices than others? What was the genetic basis of this advantageous phenotype? Why aren’t all the songbirds learning through plasticity and/or heuristics to respond differently to the sounds, when the predators themselves are not present?
To answer this, we have developed a model that aims to investigate the genetic and plastic mechanisms that underlie these fearful expressions in the songbirds’ behavior. In our model, we assume fear to be an emotion and that the emotion is coded for by a single gene. Thereby making a large number of genes into something calculable. We can therefore by this simplification investigate how the gene responds to selective pressures given by the environment in our simulations. Although this might be considered a gambit as well, by doing so we may investigate the components between the gene and fitness such as emotions, plasticity, and norm of reactions.
By using an individual-based model (IBM) with the incorporation of a genetic algorithm (Grimm, 1999; Grimm & Railsback, 2013; Holland, 1992), we suggest a bottom-up approach to investigating the proximate mechanisms behind the emotion fear. By assuming fear to be an emotion and that the emotion is coded for by a gene, we investigate how the gene responds to selective pressures given by the environment in our simulations. IBMs cannot produce theories on a systemic level (Grimm, 1999). Still, a paradigmatic model that refers to theoretical ecology is ideal for modeling. By using objects (individuals) and studying their interactions as a population, one could study how properties such as specific phenotypes emerge.
Through the use of heuristics (Hutchinson & Gigerenzer, 2005) our digital birds make decisions based on the choices made by their parents. Heuristics can be explained as certain rules of thumb, “where the proximate mechanism (the decision-making process) has an architecture that allows efficient information use and decision-making.” (Eliassen et al., 2016, p. 90). Following certain rules of thumb, the songbirds change their behavior by perceiving their environment through sensory mechanisms. In our case, the songbirds are presented with a trade-off: If they do not feed, they will reduce in mass and die of starvation, but being too bold in foraging means that they are less safe from predation. The songbirds are therefore subjected to “choosing” the ideal path, in which a simple form of heuristics is needed. These heuristics may therefore consist of building blocks (Hutchinson & Gigerenzer, 2005) that exploit learned behavior through the inheritance of genes and phenotypes. Ultimately, leading to better and quicker decision-making.
The ethics of biological computer science
The ethical reasons for using modeling and computer science in biology should also be mentioned. There are costs and benefits when invasive interventions are done to wildlife in the name of science. As great costs can be disregarded by achieving high-quality answers to important questions, one must still acknowledge the disturbance that is inflicted upon free-living wildlife. According to “The 3Rs principles within experimental animal biology” (ASAB Ethical Committee/ABS Animal Care Committee, 2023; Sneddon et al., 2017), the modeling of such events given by Allen and co-authors is suggested to be the more ethically sustainable choice of research. In the inquiry of how fear affects animals in the wild, interventions, such as Allen and co-authors (2022) presented as their research method caused the death of numerous songbirds. Even though the population regained its numbers after the intervention was removed, there are still reasons to question the ethics of this study’s interventions. Although the subject of animal welfare is sometimes criticized as not being scientifically objective, remaining agnostic of the subject would be a utilitarian approach to animals: the main reasons animals are needed are for companionship and farming (Budaev et al., 2020). Therefore, we present this model as a contribution to act against this utilitarian view of animals. By connecting animal welfare and computational biology, we hope to reduce the cost on nature in the name of science.
Materials & methods
The architecture of our model is depicted through Figure 1. For each iteration, aka generation, the digital birds are sent into an array consisting of 100 cells along the x-axis. Each cell represents a habitat consisting of two values: food availability and risk of predation. These values are randomly generated so that each cell/habitat is unique. The birds “fly” at random to a cell. The actions of the bird upon landing at a specific cell are dictated by both their gene, and how their emotional state is at that moment. If they are sufficiently afraid, they will not eat. If they are sufficiently hungry, they will not be afraid. This can either aid them in gaining mass or harm them upon meeting a predator. If they are too hungry to mind the risk of themselves being killed by the predator, they are at risk of being killed. The phenotypic range of their actions is constricted by their genetic value, which is randomly sorted throughout the population at the beginning of each simulation. Therefore, there will be a genetic diversity in place and selection of an advantageous gene will be possible.
In our model, we used elements from the theory of the global organismic state (GOS) (LeDoux, 2012) in the following ways: If our bird is beyond an emotional threshold where it becomes fully fearful, the bird will stay put and not fly from cell to cell in search for food. After a while, it will grow hungrier, and fear will reduce to a point below the threshold. Mathematically, this can be expressed in the following way:
Here, k represents the slope defining the temporal aspect of the transition between fear and hunger, and b is the intersection point of which the birds’ emotional state is at a certain point in time. Hmax and Hmin refers to “maximum hunger” and “minimum hunger” that the bird experiences. T0 is the weight-threshold of the birds and is set to -25% of the initial weight of the digital songbird. If a bird’s mass drops below this threshold, it is considered dead from starvation. Wm on the other hand, gives the value for the birds’ maximum mass, which in our model is 25% larger than its initial starting weight. We have not considered the weight of chicks since we, in our model, assume all birds to be adults.
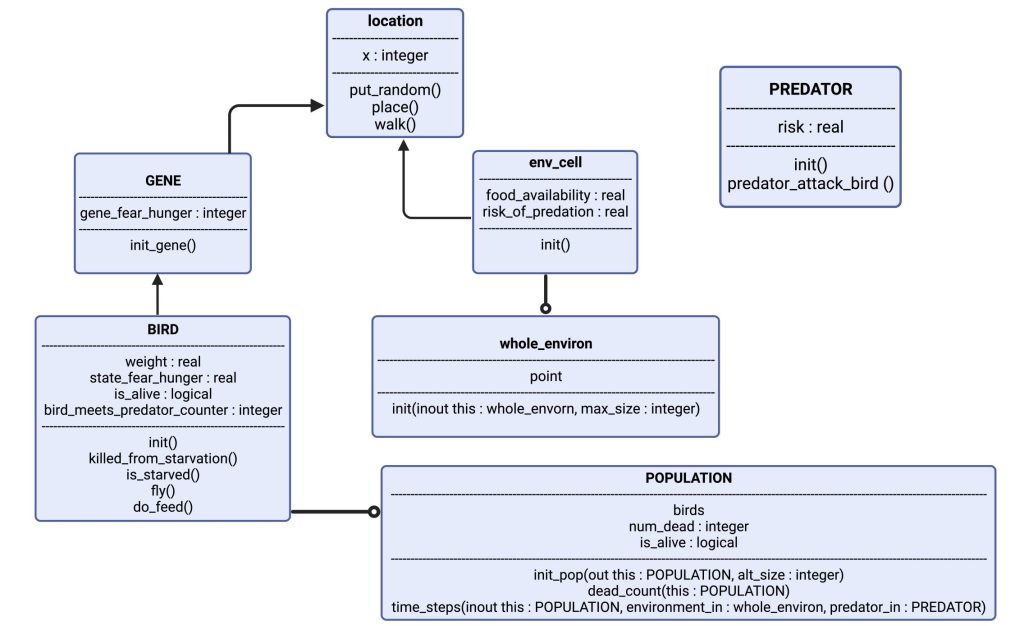
Figure 1: Visualizing the model: The object “BIRD” has attributes weight, state_fear_hunger, is_alive and a counter for when it encounters a predator. It has certain actions as well, such as: is_starved and fly. “BIRD” is controlled by “GENE”, which gives it the basis of its phenotype. “BIRD” has now a genetically defined personality, and expresses this in “location”, which is the exact point in the “env_cell” (short for environment of the cell), which is a part of “whole_environ” (the entire environment consisting of 100 cells, i.e., habitats.). In each cell there are also a few instances of “PREDATOR”, which can spawn randomly based on parameter-set probability. Each simulation spawns several thousand “BIRD”, which gives us the “POPULATION”.
Object-oriented modeling
The model consists of “objects” (figure 1). Each of the objects are representations of agents in our model, or the environment the agents act within. The agents are the songbirds (BIRD) and the predators (PREDATOR). Each of the objects have their own characteristics that define what qualities the objects possess; where the objects are (i.e., which habitat is the bird in), and how the objects’ interactions affect their state. The qualities mentioned are assigned values set by parameters in the code. An example is the object “BIRD”, which has the real value of “weight”. In the code, we set the initial weight to “20.0” (grams), which will be the initial value of the birds every time we initialize the code. By using an object-oriented model, we can better mimic the encounters a bird might have with food and risk in nature.
The Genetic Algorithm
In our model, we also created a genetic algorithm (GA) as stated by Holland (1992). When each of our objects: "Environment", "Predator" and "Parent population" (Figure 2), are initialized and iterations for each generation are done, the GA sorts the songbirds and calculates their fitness". It does so in the way illustrated by the smaller circle in Figure 2: each parent population undergoes a series of timesteps, which gives the order of their actions. After the songbirds’ actions are completed, the fitness of the remaining songbirds is calculated based on their gained mass. Of all the songbirds, 25% of the fittest are automatically chosen for reproduction by the code. To further genetic variation in the offspring generation, we have also included an additional 25% chosen at random from the remaining population. Therefore, the next generation in our model will have genes from these 50%. This process is shown in Figure 2 as “select_reproducing”. After this process of selection based on fitness, we submit our new genes to mutation. According to the literature, we chose the parameter for the mutation probability rate to be 4.6 × 10−9 (Smeds et al., 2016). The selection with added mutation results in the parent populations´ offspring (“offspring_population” in Figure 2). The offspring will become the main population for the next generation, completing our single iteration of the GA.
In our model, we chose 100 iterations of the GA, meaning we ran the simulation for 100 generations of songbirds. Since the evolution of a single gene was shown, we believe this number of generations should be sufficient. We fully acknowledge and stress the fact that this is not reality. It is however sufficient to prove that our model works and that evolution happens.
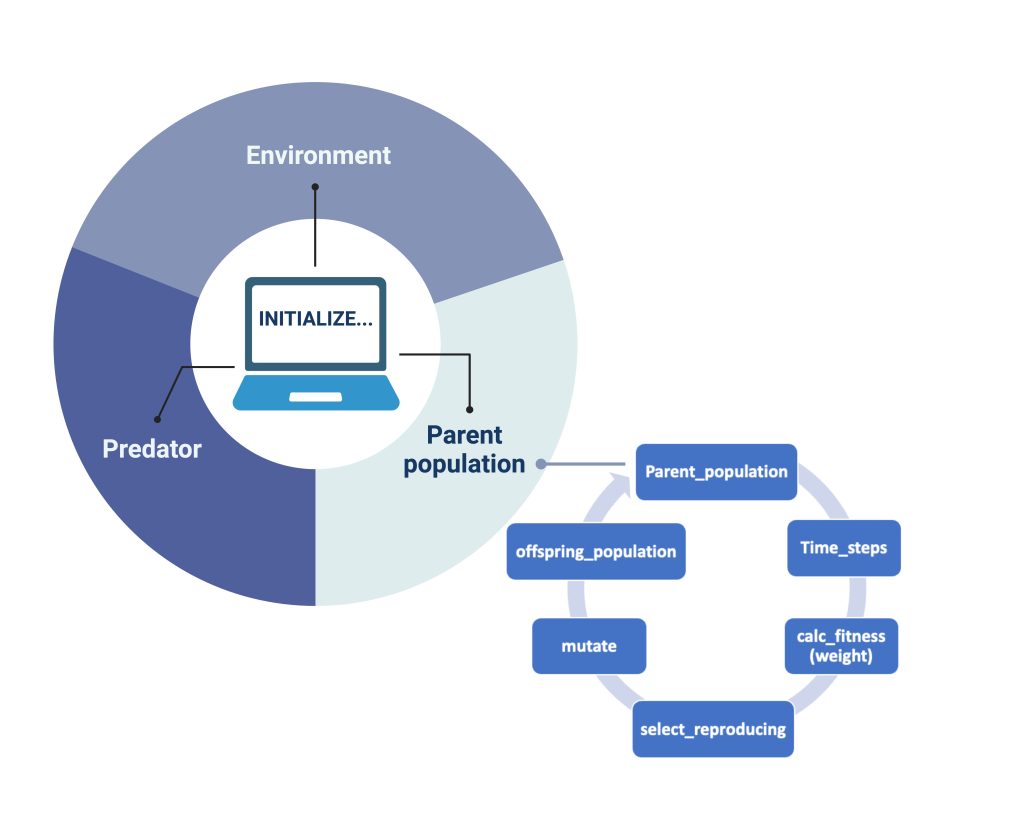
Figure 2: How the model works. For each Initialized simulation our objects (the parent population of birds, the predator and the environment interact). For the birds that show the greatest fitness (measured only by “best mass”), a selection undergoes mating and creates the offspring generation. To incorporate genetic diversity, we also select a certain number of birds that are less fit than optimal and introduce mutation of genome in each generation.
Modeling tools
Fortran (Formula Translation)
Fortran is a widely used programming language in the natural sciences, including biology. Fortran's proficiency in handling numerical calculations and array operations makes it suitable for modeling natural events and data analysis. The language provides a broad spectrum of mathematical functions and supports advanced operations, enabling biologists to develop complex models that can capture the dynamics of biological systems.
SVN (Subversion)
SVN is a version control system used in software development. With SVN, developers can work simultaneously on the same code without conflicts, as the system tracks and manages the merging of changes. It allows users to check out a working copy of the project, make modifications, and then commit those changes back to the repository. SVN maintains a comprehensive record of all changes, making it easy to roll back to previous versions if needed.
Visual Studio and Visual Studio Code
Visual Studio is a widely used integrated development environment (IDE) created by Microsoft. It provides a comprehensive set of tools and features for building a variety of software applications, including desktop, web, mobile, and cloud-based applications. Visual Studio Code is a versatile and lightweight source code editor that offers a wide range of features and customization options. Its ease of use, extensive extension ecosystem, built-in Git integration, debugging support, and productivity-enhancing tools make it a popular choice among developers for various programming languages and platforms.
The Code
The code in its entirety can be found and examined at GitHub: https://github.com/Kaw-Han/songbird-evo-model-FORTRAN. The model code can be examined, tested, run, and furthered under the restrictions of the assigned trademark.
Results & Discussion
Our findings indicate that evolution occurs rapidly in our model (Figure 3). The phenotypic expression associated with the gene in our digital songbirds is characterized by moderately cautious behavior during their search for food. This suggests that a moderate level of fear serves as a beneficial trait for increasing fitness, measured by the songbirds’ gain in mass. Figure 4a further supports this result. The population of songbirds experiences a significant decline in the first five generations, followed by a subsequent rise and stabilization. This pattern indicates the presence of selection, with the gene favored by the environment quickly dominating the population. Additionally, the graph in Figure 4c depicting the average mass of our birds contributes to our findings. It shows that the rapid growth observed in the first five generations is not sustainable; suggesting that the less fearful songbirds, which gained mass due to bold behavior, were not favored by the environment.
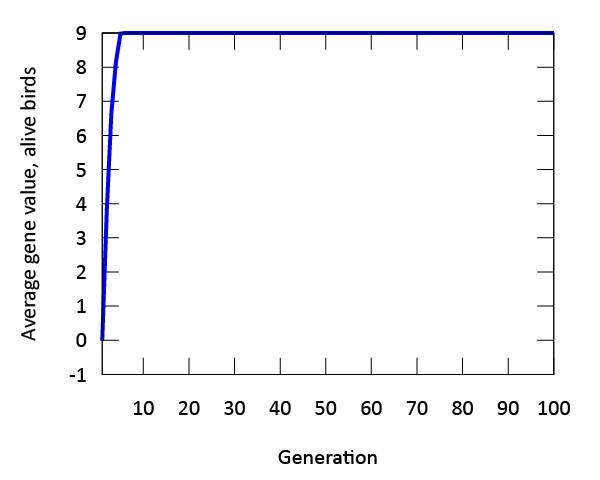
Figure 3: The genetic value "9" is evolutionary stable after approximately five generations. The phenotype expressed by this gene value is associated with moderate amounts of fear.
This point is further supported by comparing this graph to the graph in Figure 4d, which depicts the mass gain of the fittest birds. Unlike the initial increase seen in the first five generations, the graph shows a steady, linear growth rate. This indicates that the most fit songbirds are those expressing the phenotype of moderate fear (Figure 3) from the beginning of our simulation. Furthermore, the dominance of the gene is demonstrated by the standard deviation of mass in Figure 4b. As the songbirds adapt their foraging strategies through selection, the gain in mass becomes almost uniform across the population after five generations.
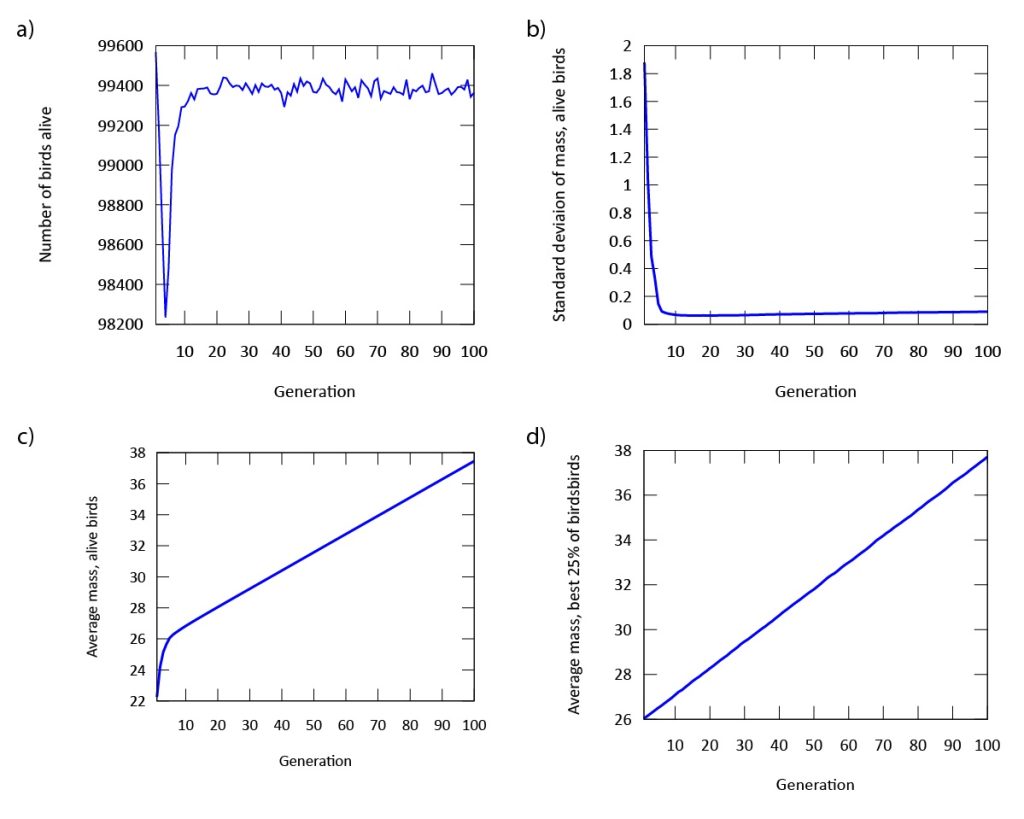
Figure 4: a) The population declines, but quickly regains its numbers after approximately five generations. b) The standard deviation of mass in our population is stabilized after approximately five generations. c) The average mass of all digital songbirds rises significantly throughout the simulation. d) The average mass of the birds with the highest fitness rises linearly and significantly throughout the simulation.
Another important finding in our model is the expression of a single gene through multiple phenotypes. When designing the digital birds with a single gene, we observed variations in the expression of this gene across the population. This plasticity, though constrained by the gene, was evident in our initial population. As time progressed in our model, evolution occurred, and the phenotypic expression we referred to as "moderate fear" remained the main phenotype. This finding is further supported by both Figures 3 and 4, which demonstrate that the fittest birds were those expressing this phenotype from the outset of our simulations.
Through our findings, we present a demonstration of how heuristics (Hutchinson & Gigerenzer, 2005) come into play. The digital birds in our study exhibited responses to predators or hunger based on the information they sensed from their environment while operating within the constraints imposed by their proximate genetic architecture. Notably, we observed variations in the responses of individuals, suggesting that the rules of thumb guiding their behavior may have limitations but are not entirely genetically predetermined. Expanding on this line of thinking, we can question how the concept of the phenotypic gambit (Grafen, 1984, 1991) explains this phenomenon. Although the gene is expressed initially in different ways, the scope of the diversity in phenotypes where still genetically limited. The phenotypic gambit does not consider that the proximate mechanisms sometimes constrain the expression of adaptive behavior, as pointed out by Fawcett et al. (2013) and is therefore sometimes wrong. The numerical findings we present add to the arguments against the simplicity of the gambit and give us cause to further investigate this phenomenon and continue questioning the benefit of the gambit’s exclusion of genetics.
While our model provides only a partial explanation, it offers valuable insights into the findings of Allen et al. (2022). In their study, the songbirds exhibited not only a significant decline in fitness but also a decrease in population size. It is worth noting that the intervention implemented in their experiment was discontinued after five generations. Interestingly, our model demonstrated a similar timeframe before the beneficial phenotype became dominant. On one hand, the fact that the model mirrored real-life events reinforces the validity and utility of the models. On the other hand, it underscores the growing significance of modeling interventions in nature as initial steps toward comprehending population dynamics and the effects of factors like predation in novel environments.
It is important to acknowledge the immediate issues raised by this thought experiment. Firstly, the ethical implications of prolonging or conducting similar experiments as Allen and co-authors (2022) on free-living populations would not align with the standards of conduct in biological science, as recognized by the ASAB Ethical Committee/ABS Animal Care Committee (2023). Secondly, adhering to animal welfare guidelines prompts further research inquiries, such as investigating the impact of invasive urbanization on wildlife inhabiting forest areas.
This underscores the growing importance of utilizing computational biology to develop models that aid in predicting likely scenarios. While models heavily rely on data obtained from field studies, they offer possibilities to explore nuances, address knowledge gaps, and even challenge established theories without sacrificing lives or causing harm to nature. In our model, we could simply design the neural capacity of the songbirds, their habitat, their physiological needs, and their psychology. By applying what we already know, we can provide information valuable for future studies. The need for such an application of our method, is best expressed by the 3Rs (ASAB Ethical Committee/ABS Animal Care Committee, 2023; Sneddon et al., 2017): Replacement, reduction and refinement. Through models and simulations, we can replace real animals with digital ones. We are then able to reduce the number of animals affected. Finally, we can refine future studies by using predictive modeling to suggest ideal points of research that affects animal life in the future.
Expanding the code
We fully acknowledge the simplicity of the model. The fitness of our birds is measured solely by their gain in mass. Although this represents successful strategies, more modules, subroutines, and functions could be interesting to include. Alternate strategies for survival and reproduction are commonly seen in nature. This would provide an interesting addition to our model. We could introduce more genes, more environmental factors such as seasonal changes or migration into the population.
In the times of environmental change, we also suggest introducing objects that represent installations placed in nature by humans. Windmills are such an object and are by many considered as intrusive to nature. Data collected from the existing sites containing windmills, can be utilized to create a valuable addition to our model, and subsequently to stake-holders on all sides of the matter.
Summary
In this article, we utilized an individual-based model (IBM) to investigate the proximate mechanisms underlying the response patterns exhibited by songbirds, as studied by Allen et al. (2022). While our understanding of the «whole picture» remains incomplete, our model offers valuable insights into how fear-based behaviors contribute to evolution. Firstly, our model demonstrated the occurrence of evolution. Our results revealed that the digital songbirds experienced an increase in body mass, leading to a higher probability of survival and reproduction. We deduced that the fittest individuals possessed phenotypes that provided advantages right from the start of our simulations. The remaining population adopted similar phenotypes within a mere few generations. Specifically, the most advantageous phenotype expressed a moderate level of fear during foraging. Secondly, our model demonstrated that multiple phenotypes could originate from the same genotype. This finding is particularly intriguing when compared to the concept known as "the phenotypic gambit" (Grafen, 1984, 1991). Although our model, like the gambit and previous models, simplifies for the sake of optimization, our findings suggest that proximate mechanisms warrant further attention from behavioral ecologists who favor the gambit's premises in their research. Finally, we propose the need for future development of our model in order to introduce more true-to-nature complexity, and therefore increase the value and precision of our simulations.
How to cite
Kawousi, H., Budaev, S. & Giske, J. (2023). The proximate mechanisms behind fear: an IBM approach to understanding behavioral changes in songbirds and the subsequent evolutionary trajectory. Bikuben 2.
References
Allen, M. C., Clinchy, M., & Zanette, L. Y. (2022). Fear of predators in free-living wildlife reduces population growth over generations. Proceedings of the National Academy of Sciences, 119(7), e2112404119. https://doi.org/10.1073/pnas.2112404119
Andersen, B. S. (2014). Effects of genetic complexity and time resolution in an individual-based model of mesopelagic fish with hunger and fear [Master thesis, The University of Bergen]. https://bora.uib.no/bora-xmlui/handle/1956/8558
ASAB Ethical Committee/ABS Animal Care Committee. (2023). Guidelines for the ethical treatment of nonhuman animals in behavioural research and teaching. Animal Behaviour, 195, I–XI. https://doi.org/10.1016/j.anbehav.2022.09.006
Budaev, S., Jørgensen, C., Mangel, M., Eliassen, S., & Giske, J. (2019). Decision-Making From the Animal Perspective: Bridging Ecology and Subjective Cognition. Frontiers in Ecology and Evolution, 7. https://www.frontiersin.org/articles/10.3389/fevo.2019.00164
Budaev, S., Kristiansen, T. S., Giske, J., & Eliassen, S. (2020). Computational animal welfare: Towards cognitive architecture models of animal sentience, emotion and wellbeing. Royal Society Open Science, 7(12), 201886. https://doi.org/10.1098/rsos.201886
Darwin, C. (1859). On the Origin of Species by Means of Natural Selection, or, the Preservation of Favoured Races in the Struggle for Life. John Murray.
Eliassen, S., Andersen, B. S., Jørgensen, C., & Giske, J. (2016). From sensing to emergent adaptations: Modelling the proximate architecture for decision-making. Ecological Modelling, 326, 90–100. https://doi.org/10.1016/j.ecolmodel.2015.09.001
Euler, L. (1767). Recherches générales sur la mortalité et la multiplication du genre humain. Mémoires de l’académie Des Sciences de Berlin, 144–164.
Fawcett, T. W., Hamblin, S., & Giraldeau, L.-A. (2013). Exposing the behavioral gambit: The evolution of learning and decision rules. Behavioral Ecology, 24(1), 2–11. https://doi.org/10.1093/beheco/ars085
Fisher, R. A. (1930). The Genetical Theory of Natural Selection. Clarendon Press.
Grafen, A. (1984). Natural selection, kin selection and group selection. In Behavioural Ecology: An Evolutionary Approach (pp. 62–84). Oxford: Blackwell Publishing. https://scholar.google.com/scholar_lookup?author=A.+Grafen+&publication_year=1984&title=%E2%80%9CNatural+selection,+kin+selection+and+group+selection,%E2%80%9D&pages=62-84
Grafen, A. (1991). Modelling in behavioural ecology. Behavioural Ecology: An Evolutionary Approach, 3, 5–31.
Grimm, V. (1999). Ten years of individual-based modelling in ecology: What have we learned and what could we learn in the future? Ecological Modelling, 115(2), 129–148. https://doi.org/10.1016/S0304-3800(98)00188-4
Grimm, V., & Railsback, S. F. (2013). Individual-based Modeling and Ecology. In Individual-based Modeling and Ecology. Princeton University Press. https://doi.org/10.1515/9781400850624
Holland, J. H. (1992). Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence. MIT Press.
Hamilton, W. D. “Selfish and Spiteful Behaviour in an Evolutionary Model.” Nature 228, no. 5277 (December 1970): 1218–20. .
Hamilton, W. D. (a) “The Genetical Evolution of Social Behaviour. I.” Journal of Theoretical Biology 7, no. 1 (1964): 1–16. https://doi.org/10.1016/0022-5193(64)90038-4.
Hamilton, W. D. (b) “The Genetical Evolution of Social Behaviour. II.” Journal of Theoretical Biology 7, no. 1 (July 1, 1964): 17–52. https://doi.org/10.1016/0022-5193(64)90039-6.
Hutchinson, J. M. C., & Gigerenzer, G. (2005). Simple heuristics and rules of thumb: Where psychologists and behavioural biologists might meet. Behavioural Processes, 69(2), 97–124. https://doi.org/10.1016/j.beproc.2005.02.019
LeDoux, J. (2012). RETHINKING THE EMOTIONAL BRAIN. Neuron, 73(4), 653–676. https://doi.org/10.1016/j.neuron.2012.02.004
Lotka, A. J. (1925). Elements of physical biology. Williams & Wilkins.
Scheiner, S. M. (1993). Genetics and Evolution of Phenotypic Plasticity. Annual Review of Ecology and Systematics, 24, 35–68.
Smeds, L., Qvarnström, A., & Ellegren, H. (2016). Direct estimate of the rate of germline mutation in a bird. Genome Research, 26(9), 1211–1218. https://doi.org/10.1101/gr.204669.116
Sneddon, L. U., Halsey, L. G., & Bury, N. R. (2017). Considering aspects of the 3Rs principles within experimental animal biology. Journal of Experimental Biology, 220(17), 3007–3016. https://doi.org/10.1242/jeb.147058
Via, S., & Lande, R. (1985). Genotype-Environment Interaction and the Evolution of Phenotypic Plasticity. Evolution, 39(3), 505–522. https://doi.org/10.2307/2408649
About the authors
 Hello and thank you for looking at my paper. My name is Hanif Kawousi and I am currently working on my master’s thesis at the Department of Biological Sciences at the University of Bergen. I believe some of the most interesting questions one could ask are within the field of evolutionary ecology. To answer these questions I am working on developing models that can simplify complex systems in real-life nature into something we can measure, handle and research, without compromising the systems’ integrity itself.
Hello and thank you for looking at my paper. My name is Hanif Kawousi and I am currently working on my master’s thesis at the Department of Biological Sciences at the University of Bergen. I believe some of the most interesting questions one could ask are within the field of evolutionary ecology. To answer these questions I am working on developing models that can simplify complex systems in real-life nature into something we can measure, handle and research, without compromising the systems’ integrity itself.
I would like to take the opportunity to thank my supervisors and co-authors: Sergey Budaev and Jarl Giske, both at Theoretical Ecology Group at UiB. I would also like to thank my wife, Jenny, for all her continuous love and support.